Regression Basics

Regression analysis allows you to infer that there is a relationship between two or more variables. These relationships are seldom exact because there is variation caused by many variables, not just the variables being studied.

Regression – A statistical Technique

Regression is a statistical technique used to analyze the relationship between two or more variables. The basic idea behind regression is to predict the value of a dependent variable based on the values of one or more independent variables. The dependent variable is also known as the response variable or outcome variable, while the independent variable is also known as the predictor variable or explanatory variable.

The most commonly used type of regression is linear regression, which involves fitting a straight line to the data. In linear regression, the dependent variable is assumed to have a linear relationship with the independent variable(s). The line of best fit is determined using a method called least squares regression, which minimizes the sum of the squared differences between the observed values and the predicted values.

 

Different Types of Regression

There are many other types of regression, including logistic regression, polynomial regression, and multiple regression. Logistic regression is used when the dependent variable is binary (i.e., only has two possible values). Polynomial regression is used when the relationship between the dependent and independent variables is not linear. Multiple regression is used when there are multiple independent variables that may be affecting the dependent variable.

 

What is regression?

Pearson’s r or Pearson’s correlation coefficient describes how strong the linear relationship between two continuous variables is. This linear correlation can be displayed by a straight line which is called regression line.

So, regression line the straight line that describe two variables best. If you can find the best fitting line in your data then it is possible to do prediction using that line equation. Using that regression line, we can predict the value ŷ for some certain value of x. But the question is how to find the regression line?

Simple regression and least squares method

How to find the regression line or how to find the best line that fitted data more accurately?

Let’s imagine that you have a scatter plot of two variables and you have drawn possible straight line through this scatterplot. That’s a huge number of lines, so in practice it will be almost impossible to do that. However, for now, imagine that you have superhuman powers and that you are able to do it. Next, you measure for every possible line the distances from the line to every case.

How to know for this below picture what line is best fit?

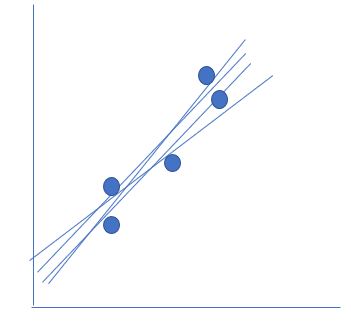
To measure the best line we first need to know about residual.

Residual  

Residual means difference between observed and predicted value. Every distance is called a residual.

See the below picture. Lets think you have a point (x1 , y1) in the scatter plot. you have the regression line  ŷ =a+bx.

So, now  ŷ1=a+bx1. Then value of residual for that observation will residual will be  y1- ŷ1.

Data = Fit + Residual

You have to calculate squared residual for all line and finally, choose the line that minimize the sum of squared residual –which is called least square error. This is call ordinary least square regression.

Once we get the best fit line that means we get the equation for Regression Line like this.

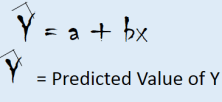
a = Intercept

b= Regression co-efficient

 

Slope and Intercept

In the regression equation the constant part a is called intercept and b is called slope or regression co-efficient. Below diagram shows what is slope and what is Regression Co-efficient.

If you consider the below picture then in left side picture line 1 & 2 both has same slope but intercept is different whereas right side picture has same intercept with different slope.

Prediction Using Regression Formula

Now if we have the regression line formula then it is possible to predict some Y-hat value for unknown x value.

 

Estimating  Regression Parameter

In practice it is almost impossible to draw every possible line and to compute for every single possible line all the residuals. Luckily, mathematicians have found a trick to find the regression line. I won’t explain how this trick works here, because it is rather complicated. For now it suffices to know that it is based on minimizing the sum of the squared residuals.

Usually the computer finds the regression line for you, so you don’t have to compute it yourself. However, when you know the means and standard deviations of your variables and the corresponding Pearson’s r correlation coefficient, you can compute the regression equation by means of two formulas.

Here are the formulas for estimating the regression parameter slope (b) and interpret (a). Please keep in mind that x̅ and y̅ are the mean of independent and dependent variable. r is the correlation coefficient or pearson’s r and sy and sx are standard deviation of your x and y variable.

Once you are doing prediction it is very important to know strength of fit for your regression line.

We have studied Pearson’s r in previous page which explains direction and strength of a relation. If we take square of Pearson’s r that means R^2 which tells us how much better a regression line predicts the value of a dependent variable to than the mean of that variable. This is called R-Square measured measure.

• Always keep in mind that interpretation of Pearson’s r and R^2 is different. R^2 is always a positive number which give you two information given below.

How to interpret the R-Square?

• If R^2= 0.71. It’s  mean that prediction error is 71 % smaller than when you use mean.
• On the other way, it explains the amount of variance in your dependent variable (Y) that is explained by your independent variable X.

If you are reading it first time, it might be little confusing to you. So, to get better understanding read the below example carefully.

Example

Social scientists have shown that a leader’s physical height is related to his or her success. Suppose you want to test if you can replicate this result. To do that, you look at the heights and the average approval ratings of the four most recent presidents of the United States. You employ this data matrix and your goal is to answer 4 related questions:

(1) is there a linear relationship between the two variables?

(2) what is the size of Pearson’s r correlation coefficient?

(3) what do the regression equation and the regression line look like? And

(4) what is the size of r-squared?

Let’s start with the first question:

Is there a linear relationship between the two variables?

To answer that question, you make a scatterplot. To make a scatterplot, you must first decide what’s the dependent variable and what’s the independent variable. In this case it’s more likely that a leader’s physical height influences his or her approval ratings than that approval ratings affect a leader’s height. After all, we don’t expect a leader to become taller once his or her approval rates get better… So, the independent variable height goes on the x-axis, and the dependent variable approval rating on the y-axis. Based on the minimum and maximum values of our variables we scale our axes. Our independent variable height ranges from 182 centimeters to 188 centimeters. You therefore use a scale from 180 to 190 centimeters. Your dependent variable ranges from 47 through 60.9. You therefore scale this axis from 45 through 65. Next, we decide, based on our data matrix, where we should position the 4 presidents. Obama is 185 centimeters tall and has an approval rating of 47. Bush junior has a physical height of 182 centimeters and an average approval rating of 49.9. Clinton and Bush senior’s heights are 188 centimeters and approval rates are 55.1 and 60.9 respectively.

 

Now, You can answer the first question: Yes, there seems to be a linear relationship between a leader’s height and his approval rating. The line describing this relationship goes up, which means that the correlation between the two variables is positive.

The second question is what the value of Pearson’s r is.

To compute Pearson’s r we need the formula. To start with, you need to compute all the z-scores of both your independent and your dependent variable. To do that you need the means and standard deviations of these variables. The mean of the independent variable height is 185.75 centimeters and the standard deviation is 2.87 centimeters. The mean approval rating (the dependent variable in our study) is 53.23 and the standard deviation is 6.12. First we compute the z-scores for our independent variable by subtracting the mean from every original score and then dividing the outcome by the standard deviation. We do that here: 185 minus 185.75 divided by 2.87. That makes -0.26132. We also do that for the other scores. Here are the results. We then repeat that for the dependent variable. 47 minus 53.23 divided by 6.11 makes – 1.01964. And we do that for the other cases too. The next step is to multiply the z-scores of every case with each other. For the first case this results in -0.26132 multiplied with -1.01964. That makes 0.266456 and so on. We have now finished this part of the formula. Next we have to add up all these values. That makes 2.202649. Finally, we have to divide by n minus 1. Our n is 4, so n minus 1 equals 4 minus 1 is 3. The result, rounded up, is 0.73. That is our Pearson’s r. This indicates that there is a rather strong and positive linear correlation between a leader’s body height and his average approval rating.

The next step is to find the regression equation.

The computer finds the regression line by looking for the line that minimizes the sum of the squared residuals. You do not have to do this yourself. Luckily this complicated procedure boils down to two rather simple formulas. One formula to compute the regression coefficient (this one), and one formula to compute the intercept (this one). Together these formulas give you your regression line. We already have all our necessary ingredients. So now you can use the formulas. The regression slope is 0.73 multiplied with 6.11 divided by 2.87. That makes 1.56. The intercept is 53.23 minus 1.56 multiplied with 185.75. That makes -237.11. The regression equation is y-hat minus 237.11 plus 1.56 times X. The intercept indicates that the predicted y-value is minus -237.11 when x is 0. This number has no substantive meaning because a physical height of 0 meter is impossible. The intercept only serves mathematical purposes: it makes it possible to draw the line. With the regression equation found, we can predict the value of dependent variable when independent variable equals 182 centimeters (the minimum value in our sample). That’s -237.11 plus 1.56 times 182. That makes 46.81. That’s here.

You can also do that for maximum value: that’s *-237.11 plus 1.56 multiplied with 188. That’s 56.17. That’s here. You can now draw the regression line. This line is the straight line that best represents the linear relationship between X and Y. It is the line for which the sum of the squared residuals is the smallest. We can, of course, predict y-values for every possible x-value. All these predicted y-values, or y-hat’s, are located on the regression line.

The fourth question is what the value of r-squared is.

That’s easy. It’s Pearson’s r squared. So: 0.73 multiplied with 0.73 equals 0.53. But how should you interpret this number? Well, you can say that the prediction error is 53 per cent smaller when you use the regression line than when we employ the mean of the dependent variable. You can also say that 53 per cent of the variation in the dependent variable is explained by your independent variable. So, we learnt that tall leaders are more successful than short leaders. However… This conclusion is based on a sample of only 4 American presidents who don’t differ much from each other when it comes to their physical height. It is up to you to decide if this warrants far-reaching inferences about the relationship between height and approval ratings.
However, for at least two reasons, we need to be very careful when we interpret the results. The first reason is that on the basis of a regression analysis, we can never prove that there is a causal relationship between two variables. We can, in other words, never be certain that one variable is the cause of another variable. This translates to one single and not very complicated, but extremely important message: correlation is no causation.

Summary

Regression analysis is commonly used in fields such as economics, finance, psychology, and epidemiology, among others, to analyze data and make predictions about future outcomes. Simple linear regression helps researchers estimate parameters of linear equations connecting variables, making it easier to predict dependent variable values in different conditions. It also emphasizes the importance of isolating the effect of one independent variable on the dependent variable for decision-making and policy design. Regression is a powerful statistical tool used in various fields, and while the concept behind it is simple, the mathematics can be complex, and researchers often use computers to find regression equations.